写在前面

分站主题比较简约，所以把算法作业的内容搬运了过来，方便喜欢简约风格的人来查看。

二叉树的中序遍历

大一 -> 大二暑期算法作业

分站已经上线简约风算法作业集合

看到题目的感想

被离散数学折磨之后看见树就会想到离散数学，虽然学习离散数学的时候老师教过中序遍历，但是看到这个题的时候还是没有想起来中序遍历是个啥，索性就去搜索了一下（快进到被老师打死）。

附上百度百科链接：

中序遍历：https://baike.baidu.com/item/%E4%B8%AD%E5%BA%8F%E9%81%8D%E5%8E%86

题目描述

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[2,1]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal

题目解答

（ps：由于做题时采用的是执行代码，并未提交，提交结果均为后来补上，所以时间均为两天前）

1.递归算法

利用递归的思想解题也是老朋友了，在之前的算法题里面有过接触，所以并不是很难理解。

（1）解题思路

在解题的时候，了解到了一个名叫 vector 的东西，可以理解为C++和Java中的一种动态数组。记得第一次听到这个名词的时候还是在翁恺老师的《C语言程序设计》这门课上听到的，想想还真是怀念。（跑远了

附上一些链接（配合梯子一起食用）：

vector：内存在堆上

注意：vector每添加一次都会把之前的全复制一遍，所以效率并不高。

1） https://docs.microsoft.com/zh-cn/cpp/standard-library/vector-class?view=msvc-160 来源：Microsoft C++、C 和汇编程序文档

2） https://docs.oracle.com/en/java/javase/16/docs/api/jdk.incubator.vector/jdk/incubator/vector/package-summary.html 来源：Java官方文档里的包（纯英文比较难顶

3） https://baike.baidu.com/item/Vector/3330482 来源：百度百科

4） https://www.w3cschool.cn/cpp/cpp-i6da2pq0.html 来源：某不知名C++教程

《C语言程序设计》：https://www.icourse163.org/learn/ZJU-9001?tid=9001#/learn/announce 来源：中国大学MOOC

本题可以通过递归思想对给出的二叉树的左子树、根节点、右子树依次进行遍历（中序遍历），并将各个数据存放在设置好的vector中（由于vector是动态分配内存的，所以比用担心大小会不够用），最后即可得到该二叉树的中序遍历。

（2）代码

解题代码如下（配合题目链接食用）：

C++

有一种比较好用的C++容器，比vector好用，只是不能自增。（本题未使用）

array：内存在栈上

array： http://c.biancheng.net/view/6688.html 来源：C语言中文网

array： https://www.bilibili.com/video/BV18b4y1X7EB?from=search&seid=11718690349134275715 来源：哔哩哔哩（是一个油管的小哥哥，讲的很棒，圈粉了）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    void inorder(TreeNode* root, vector<int>& res) {
        if (!root) { // 如果碰到空节点，说明该部分遍历已完成，return出去
            return;
        }
        inorder(root->left, res); // 递归遍历左子树
        res.push_back(root->val); // 将该节点的值增加在动态数组末尾
        inorder(root->right, res); // 递归遍历右子树
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res; // 新建一个int类型的vector,用来存放遍历结果
        inorder(root, res); // 从根节点root开始遍历，依次放入值
        return res; // 返回遍历结果
    }
};

Java

List & ArrayList 是Java中的一种列表。

List & ArrayList：https://www.jianshu.com/p/25aa92f8d681 来源：简书

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>(); // 新建Integer的List来存放数值
        inorder(root, res); // 从根节点root开始遍历，依次将数值放入
        return res; // 返回遍历结果
    }

    public void inorder(TreeNode root, List<Integer> res) {
        if (root == null) { // 如果碰到空节点，说明该部分遍历已完成，return出去
            return;
        }
        inorder(root.left, res); // 递归遍历左子树
        res.add(root.val); // 将该节点的值增加在末尾
        inorder(root.right, res); // 递归遍历右子树
    }
}

C（来自题解）

（C语言中的动态数组不会玩，于是把题解拿过来）

C语言动态数组 https://www.runoob.com/w3cnote/c-dynamic-array.html 来源：菜鸟教程

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

void inorder(struct TreeNode* root, int* res, int* resSize) {
    if (!root) {
        return;
    }
    inorder(root->left, res, resSize);
    res[(*resSize)++] = root->val;
    inorder(root->right, res, resSize);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int* res = malloc(sizeof(int) * 501);
    *returnSize = 0;
    inorder(root, res, returnSize);
    return res;
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（3）总结

利用递归思想来解题还是比较舒服的，也很好用，适合我这种菜鸡。

2.迭代算法

关于迭代算法的基本思想：

迭代算法 https://www.cnblogs.com/cs-whut/p/11024564.html 来源：博客园

迭代算法之前没有接触过，上手有点看不懂。

（1）解题思路

通过迭代 + 栈模型来清楚的展现解题流程（题解中有动画展示，配合食用比较好理解）。

（2）代码

解题代码如下（配合题目链接食用）：

C++

C++的栈：

stack http://c.biancheng.net/view/478.html 来源：C语言中文网

stack https://www.apiref.com/cpp-zh/cpp/container/stack.html 来源：C++文档

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res; // 新建一个int类型的vector,用来存放遍历结果
        stack<TreeNode*> stk; // 新建栈
        while (root != nullptr || !stk.empty()) { // 节点有数值 或 栈不为空
            while (root != nullptr) { // 当节点有值时
                stk.push(root); // 数据入栈
                root = root->left; // 访问左子树
            }
            root = stk.top(); // 找到栈顶数据的节点
            // top()：返回一个栈顶元素的引用，类型为 T&。如果栈为空，返回值未定义。
            stk.pop();
            // pop()：弹出栈顶元素。
            res.push_back(root->val); // 在vector末尾添加当前节点数据
            root = root->right; // 访问右子树
        }
        return res; // 返回结果
    }
};

Java

Java的栈：

Deque： https://www.jianshu.com/p/d78a7c982edb 来源：简书

stack：**

（1） https://www.javatpoint.com/java-stack 来源：某Java文档

（2） https://blog.csdn.net/YQYnsmile/article/details/78457539 来源：屑C某某N

（3） https://docs.oracle.com/en/java/javase/16/docs/api/java.base/java/util/Stack.html 来源：某全英文Java文档

Deque可以作为堆栈（LIFO后进先出），此接口优于传统Stack类的使用。

Stack和Deque方法的比较

栈方法	等效Deque方法
push(e)	addFirst(e)
pop()	removeFirst()
peek()	peekFirst()

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>(); // 新建List来保存数据
        Deque<TreeNode> stk = new LinkedList<TreeNode>(); // 新建栈
        while (root != null || !stk.isEmpty()) { // 节点有数值 或 栈不为空
            while (root != null) { // 节点有数值时
                stk.push(root); // 将数据放入栈
                root = root.left; // 访问左子树
            }
            root = stk.pop(); // pop()：弹出栈顶元素。
            res.add(root.val); // 在List末尾添加当前节点数据
            root = root.right; // 访问右子树
        }
        return res; // 返回结果
    }
}

C（来自题解）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    int* res = malloc(sizeof(int) * 501);
    struct TreeNode** stk = malloc(sizeof(struct TreeNode*) * 501);
    int top = 0;
    while (root != NULL || top > 0) {
        while (root != NULL) {
            stk[top++] = root;
            root = root->left;
        }
        root = stk[--top];
        res[(*returnSize)++] = root->val;
        root = root->right;
    }
    return res;
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（3）总结

利用迭代算法来解题的思想还没有怎么接触过没上手感觉比较难。（还是递归香 确信）

3.Morris 中序遍历（来自题解）

这个就是真的闻所未闻了，看了题解，决定搬过来

（1）思路与算法

Morris 遍历算法是另一种遍历二叉树的方法，它能将非递归的中序遍历空间复杂度降为 O(1)O(1)。

Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 xx）：
如果 xx 无左孩子，先将 xx 的值加入答案数组，再访问 xx 的右孩子，即 x = x . right。
如果 xx 有左孩子，则找到 xx 左子树上最右的节点（即左子树中序遍历的最后一个节点，xx 在中序遍历中的前驱节点），我们记为 predecessor。根据 predecessor 的右孩子是否为空，进行如下操作。
- 如果 predecessor 的右孩子为空，则将其右孩子指向 xx，然后访问 xx 的左孩子，即 x = x . left。
- 如果 predecessor 的右孩子不为空，则此时其右孩子指向 xx，说明我们已经遍历完 xx 的左子树，我们将 predecessor 的右孩子置空，将 xx 的值加入答案数组，然后访问 xx 的右孩子，即 x = x . right。
重复上述操作，直至访问完整棵树。

4.其实整个过程我们就多做一步：假设当前遍历到的节点为 xx，将 xx 的左子树中最右边的节点的右孩子指向 xx，这样在左子树遍历完成后我们通过这个指向走回了 xx，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

（2）代码

题解链接： https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/ 来源：力扣

不想搬运代码了，就给出了链接。Morris 中序遍历是题解中的第三种解法，题解带有动画教程，可以看看。

（3）总结

一种没听过的中序遍历算法，搬运题解来的。（主要还是太菜了没玩明白）

题目总结

此次题目中，出现了递归算法、迭代算法、Morris 遍历算法三种解题思路。

总的来说，还是递归较好理解，写起来难度稍微低一些；迭代算法初次了解，试了试水；Morris 遍历算法第一次见，还是看题解叭（还是人菜）。

爬楼梯

大一 -> 大二暑期算法作业

本文档中有对动态规划的解读（来自题解）

分站已经上线简约风算法作业集合

看到题目的想法

这是一道比较经典的题目，之前好像见过类似的题目，所以上手还是有一些思路的。

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶

示例 2：

输入： 3
输出： 3
解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/climbing-stairs
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目解答

（ps：由于做题时采用的是执行代码，并未提交，提交结果均为后来补上，所以时间均为两天前）

1.动态规划

（1）解题思路

刚开始事项用递归写一下的，后来发现递归会超时，于是选用了动态规划。

这是一道典型的动态规划题，由于每步只能走一或两阶台阶，所以到达这一阶的方法数是跨一阶到达 + 跨两阶到达。所以走到第一阶有一种方法，走到第二阶有两种方法，从第三阶开始，每一阶的方法数等于前两阶的方法数的代数和（跨一阶到达 + 跨两阶到达）（ps：可以用数组储存，但没必要，因为我们需要的是最终结果。

（有斐波那契那味了。

（2）代码

由于思路比较简单，也是顺利的写出了代码。（配合题目链接食用）

C++

class Solution {
public:
    int climbStairs(int n) {
        int p = 0, q = 0, r = 1; // 初始化
        for (int i = 1; i <= n; ++i) { // 遍历计算直到算出想要的结果
            p = q; 
            q = r; 
            r = p + q;
        }
        return r; // 返回想要的结果
    }
};

Java

class Solution {
    public int climbStairs(int n) {
        int p = 0, q = 0, r = 1; // 初始化
        for (int i = 1; i <= n; ++i) { // 遍历计算直到算出想要的结果
            p = q; 
            q = r; 
            r = p + q;
        }
        return r; // 返回想要的结果
    }
}

C

int climbStairs(int n) {
    int p = 0, q = 0, r = 1; // 初始化
    for (int i = 1; i <= n; ++i) { // 遍历计算直到算出想要的结果
        p = q;
        q = r;
        r = p + q;
    }
    return r; // 返回想要的结果
}

（3）总结

这样直接计算的方法思路很简单，但是问题是计算的结果无法保留，用一次就要重新计算一次，十分的不方便。

2.斐波那契数列

（1）解题思路

不难看出，此题的数据就是我们熟悉的斐波那契数列，因此我们可以借助斐波那契数列的通项公式来快速算出我们想要的结果（前一种解发是从头计算出来的，台阶数较大时效率低。

这种方法简单粗暴，就是通项公式不好记。

通项公式的推导过程就不写了，可以去题解里面看一下。+

题目链接（去看官方题解）：https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/

（2）代码

C++

class Solution {
public:
    int climbStairs(int n) {
        double sqrt5 = sqrt(5);
        double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1); // 斐波那契数列通项公式
        return (int)round(fibn / sqrt5); // 返回结果
    }
};

Java

public class Solution {
    public int climbStairs(int n) {
        double sqrt5 = Math.sqrt(5);
        double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1); // 斐波那契数列通项公式
        return (int) Math.round(fibn / sqrt5); // 返回结果
    }
}

C

int climbStairs(int n) {
    double sqrt5 = sqrt(5);
    double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1); // 斐波那契数列通项公式
    return (int) round(fibn / sqrt5); // 返回结果
}

（3）总结

这种解决办法方便快捷，也不会浪费多余的时间空间来计算，比较好用。（缺点就是通项公式并不容易记住）

3.矩阵快速幂（来自题解）

（1）解题思路 + 代码

说实话，行看到这种方法的时候感觉回到了线性代数的课堂上，又是熟悉的矩阵操作，让人头疼

具体的解题思路和代码就不搬过来了，可以去官方题解下查看。

题目链接（去看官方题解）：https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/

（2）总结

利用矩阵运算解题的方法还是没见过的，对我来说比较新奇，还需要认真的研究研究。

题目总结

这道题的难度中规中矩，但也会有很奇妙很方便的解决方案，也让我知道了运用矩阵运算来解题的方法，很棒。

拓展（动态规划）（摘自题解）

本部分附带原作者对本题的总结

不少同学对动态规划还处于朦胧状态，我特意录了一期视频，讲一讲动态规划解题方法论，这里详细介绍了动规五部曲，相信结合本篇题解，会对你学习动态规划有所帮助。

视频链接：https://www.bilibili.com/video/BV13Q4y197Wg)

做动规题目的时候，很多同学会陷入一个误区，就是以为把状态转移公式背下来，照葫芦画瓢改改，就开始写代码，甚至把题目AC之后，都不太清楚dp[i]表示的是什么。

这就是一种朦胧的状态，然后就把题给过了，遇到稍稍难一点的，可能直接就不会了，然后看题解，然后继续照葫芦画瓢陷入这种恶性循环中。

状态转移公式（递推公式）是很重要，但动规不仅仅只有递推公式。

对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

一些同学可能想为什么要先确定递推公式，然后在考虑初始化呢？

因为一些情况是递推公式决定了dp数组要如何初始化！

后面的讲解中我都是围绕着这五点来进行讲解。

可能刷过动态规划题目的同学可能都知道递推公式的重要性，感觉确定了递推公式这道题目就解出来了。

其实确定递推公式仅仅是解题里的一步而已！

一些同学知道递推公式，但搞不清楚dp数组应该如何初始化，或者正确的遍历顺序，以至于记下来公式，但写的程序怎么改都通过不了。

后序的讲解的大家就会慢慢感受到这五步的重要性了。

动态规划应该如何debug

相信动规的题目，很大部分同学都是这样做的。

看一下题解，感觉看懂了，然后照葫芦画瓢，如果能正好画对了，万事大吉，一旦要是没通过，就怎么改都通过不了，对 dp数组的初始化，递归公式，遍历顺序，处于一种黑盒的理解状态。

写动规题目，代码出问题很正常！

找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！

一些同学对于dp的学习是黑盒的状态，就是不清楚dp数组的含义，不懂为什么这么初始化，递推公式背下来了，遍历顺序靠习惯就是这么写的，然后一鼓作气写出代码，如果代码能通过万事大吉，通过不了的话就凭感觉改一改。

这是一个很不好的习惯！

做动规的题目，写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。

然后再写代码，如果代码没通过就打印dp数组，看看是不是和自己预先推导的哪里不一样。

如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。

如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。

这样才是一个完整的思考过程，而不是一旦代码出问题，就毫无头绪的东改改西改改，最后过不了，或者说是稀里糊涂的过了。

这也是我为什么在动规五步曲里强调推导dp数组的重要性。

举个例子哈：在「代码随想录」刷题小分队微信群里，一些录友可能代码通过不了，会把代码抛到讨论群里问：我这里代码都已经和题解一模一样了，为什么通过不了呢？

发出这样的问题之前，其实可以自己先思考这三个问题：

这道题目我举例推导状态转移公式了么？
我打印dp数组的日志了么？
打印出来了dp数组和我想的一样么？

如果这灵魂三问自己都做到了，基本上这道题目也就解决了，或者更清晰的知道自己究竟是哪一点不明白，是状态转移不明白，还是实现代码不知道该怎么写，还是不理解遍历dp数组的顺序。

然后在问问题，目的性就很强了，群里的小伙伴也可以快速知道提问者的疑惑了。

注意这里不是说不让大家问问题哈，而是说问问题之前要有自己的思考，问题要问到点子上！

大家工作之后就会发现，特别是大厂，问问题是一个专业活，是的，问问题也要体现出专业！

如果问同事很不专业的问题，同事们会懒的回答，领导也会认为你缺乏思考能力，这对职场发展是很不利的。

所以大家在刷题的时候，就锻炼自己养成专业提问的好习惯。

总结

这一篇是动态规划的整体概述，讲解了什么是动态规划，动态规划的解题步骤，以及如何debug。

动态规划是一个很大的领域，今天这一篇讲解的内容是整个动态规划系列中都会使用到的一些理论基础。

在后序讲解中针对某一具体问题，还会讲解其对应的理论基础，例如背包问题中的01背包，leetcode上的题目都是01背包的应用，而没有纯01背包的问题，那么就需要在把对应的理论知识讲解一下。

大家会发现，我讲解的理论基础并不是教科书上各种动态规划的定义，错综复杂的公式。

这里理论基础篇已经是非常偏实用的了，每个知识点都是在解题实战中非常有用的内容，大家要重视起来哈。

原作者对本题总结

这道题目和动态规划：斐波那契数题目基本是一样的，但是会发现本题相比动态规划：斐波那契数难多了，为什么呢？

关键是动态规划：斐波那契数题目描述就已经把动规五部曲里的递归公式和如何初始化都给出来了，剩下几部曲也自然而然的推出来了。

而本题，就需要逐个分析了，大家现在应该初步感受出关于动态规划，你该了解这些！里给出的动规五部曲了。

简单题是用来掌握方法论的，例如昨天斐波那契的题目够简单了吧，但昨天和今天可以使用一套方法分析出来的，这就是方法论！

所以不要轻视简单题，那种凭感觉就刷过去了，其实和没掌握区别不大，只有掌握方法论并说清一二三，才能触类旁通，举一反三哈！

原作者的题目解答

原作者的题目解答：https://leetcode-cn.com/problems/climbing-stairs/solution/dai-ma-sui-xiang-lu-dong-tai-gui-hua-jin-y1hw/

罗马数字转整数

大一 -> 大二暑期算法作业

分站已经上线简约风算法作业集合

看到题目的想法

这个题目看起来挺有意思的，但是好像不好解。

题目描述

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例 1:

输入: “III”
输出: 3

示例 2:

输入: “IV”
输出: 4

示例 3:

输入: “IX”
输出: 9

示例 4:

输入: “LVIII”
输出: 58

解释: L = 50, V= 5, III = 3.

示例 5:

输入: “MCMXCIV”
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

1 <= s.length <= 15
s 仅含字符 (‘I’, ‘V’, ‘X’, ‘L’, ‘C’, ‘D’, ‘M’)
题目数据保证 s 是一个有效的罗马数字，且表示整数在范围 [1, 3999] 内
题目所给测试用例皆符合罗马数字书写规则，不会出现跨位等情况。
IL 和 IM 这样的例子并不符合题目要求，49 应该写作 XLIX，999 应该写作 CMXCIX 。
关于罗马数字的详尽书写规则，可以参考罗马数字 - Mathematics 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/roman-to-integer
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目解答

（ps：由于做题时采用的是执行代码，并未提交，提交结果均为后来补上，所以时间均为两天前）

1.暴力解题

（1）解题思路

想了想还是选择了暴力解题（比较简单。

将特殊情况转为另一个不在 I， V， X， L，C，D 和 M 中的单独的字母；再重新挨个求和。

（2）代码

配合题目链接食用

C++

earse：C++中string erase函数的使用(转载) - jackdesk - 博客园 (cnblogs.com)

class Solution {
public:
    int romanToInt(string s) {
        int sum=0;
    for(int i=0;i<s.size();i++) // 将特殊情况转换
    {
        if(s[i]=='I'&&s[i+1]=='V')
        {
            s.erase(i+1,1);
            s[i]='H';
        }
        else if(s[i]=='I'&&s[i+1]=='X')
        {
            s.erase(i+1,1);
            s[i]='J';
        }
        else if(s[i]=='X'&&s[i+1]=='L')
        {
            s.erase(i+1,1);
            s[i]='O';
        }
        else if(s[i]=='X'&&s[i+1]=='C')
        {
            s.erase(i+1,1);
            s[i]='Q';
        }
        else if(s[i]=='C'&&s[i+1]=='D')
        {
            s.erase(i+1,1);
            s[i]='A';
        }
        else if(s[i]=='C'&&s[i+1]=='M')
        {
            s.erase(i+1,1);
            s[i]='B';
        }
    }
    for(int i=0;i<s.size();i++) // 挨个求和
    {
        switch(s[i])
        {
            case 'I':{
                sum+=1;
                break;
            }
            case 'V':{
                sum+=5;
                break;
            }
            case 'X':{
                sum+=10;
                break;
            }
            case 'L':{
                sum+=50;
                break;
            }
            case 'C':{
                sum+=100;
                break;
            }
            case 'D':{
                sum+=500;
                break;
            }
            case 'M':{
                sum+=1000;
                break;
            }
            case 'H':{
                sum+=4;
                break;
            }
            case 'J':{
                sum+=9;
                break;
            }
            case 'O':{
                sum+=40;
                break;
            }
            case 'Q':{
                sum+=90;
                break;
            }
            case 'A':{
                sum+=400;
                break;
            }
            case 'B':{
                sum+=900;
                break;
            }
        }
    }
    return sum;
    }
};

（3）总结

暴力计算的方法想起来并不复杂，但是写起来麻烦（重复、相似比较多），而且代码的性能也不高，所以还是不建议采用暴力算法。

2.模拟（来自题解）

很巧妙的一种方法，看完之后情不自禁的妙了起来。

妙~啊~~

官方题解：https://leetcode-cn.com/problems/roman-to-integer/solution/luo-ma-shu-zi-zhuan-zheng-shu-by-leetcod-w55p/

（1）解题思路

通常情况下，罗马数字中小的数字在大的数字的右边。若输入的字符串满足该情况，那么可以将每个字符视作一个单独的值，累加每个字符对应的数值即可。

例如 XXVII 可视作 X+X+V+I+I=10+10+5+1+1=27。

若存在小的数字在大的数字的左边的情况，根据规则需要减去小的数字。对于这种情况，我们也可以将每个字符视作一个单独的值，若一个数字右侧的数字比它大，则将该数字的符号取反。

例如 XIV 可视作 X−I+V=10−1+5=14。

（2）代码

这里用到了map这个东西，可以看看

C++

C++map： https://www.w3cschool.cn/cpp/cpp-fu8l2ppt.html 来源：某 C ++文档

class Solution {
private:
    map<char, int> symbolValues = {
        {'I', 1},
        {'V', 5},
        {'X', 10},
        {'L', 50},
        {'C', 100},
        {'D', 500},
        {'M', 1000},
    };

public:
    int romanToInt(string s) {
        int ans = 0;
        int n = s.length();
        for (int i = 0; i < n; ++i) {
            int value = symbolValues[s[i]];
            if (i < n - 1 && value < symbolValues[s[i + 1]]) {
                ans -= value;
            } else {
                ans += value;
            }
        }
        return ans;
    }
};

Java

java map：https://blog.csdn.net/qq_29373285/article/details/81487594

class Solution {
    Map<Character, Integer> symbolValues = new HashMap<Character, Integer>() {{
        put('I', 1);
        put('V', 5);
        put('X', 10);
        put('L', 50);
        put('C', 100);
        put('D', 500);
        put('M', 1000);
    }};

    public int romanToInt(String s) {
        int ans = 0;
        int n = s.length();
        for (int i = 0; i < n; ++i) {
            int value = symbolValues.get(s.charAt(i));
            if (i < n - 1 && value < symbolValues.get(s.charAt(i + 1))) {
                ans -= value;
            } else {
                ans += value;
            }
        }
        return ans;
    }
}

（3）总结

很巧妙地方法，是我没想到的，很棒。

题目总结

听题解说是很经典的字符串匹配的题目，感觉很有意思，就是没有想到巧妙地方法。需要再接再厉。

太平洋大西洋水流问题

大一 -> 大二暑期算法作业

分站已经上线简约风算法作业集合

看到题目的感想

刚看到这个题目的时候感觉他不是很熟悉，没有见过类似的题目，也没有见过类似的场景，感觉有点意思。

题目不算很长，但感觉难度不小。

题目描述

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

提示：

输出坐标的顺序不重要
m 和 n 都小于150

示例：

给定下面的 5x5 矩阵:

太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5) /
~ 3 2 3 (4) (4) /
~ 2 4 (5) 3 1 /
~ (6) (7) 1 4 5 /
~ (5) 1 1 2 4 /

/ / / / / 大西洋

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元). （序号先左后上）

题目解答

（ps：由于做题时采用的是执行代码，并未提交，提交结果均为后来补上，所以时间均为两天前）

逆流而上

最开始的名字叫逆着水流向上找，后面才想起来有逆流而上这个成语，才改了名字。

最开始浮现的思路是想暴力解题，后来发现暴力解题太过于麻烦，效率也不高，索性就放弃了。之后才有的现在这个想法。

（1）解题思路

本题找的是能够让水流留到两片水域的陆地单元的位置坐标，那么既然水能过去，那我们反过来找，分别找到两个水域的水能流到的地方，之后取交集，就得到了我们想要的答案。

（2）代码

配合题目链接食用

Java

注：这个代码在idea上可以正常运行，但在力扣上会有报错。报错如下：

error: incompatible types: List<int[]> cannot be converted to List<List> [in Driver.java]

List<List> ret = new Solution().pacificAtlantic(param_1);

List & ArrayList：https://www.jianshu.com/p/25aa92f8d681 来源：简书

class Solution {

            public List<int[]> pacificAtlantic(int[][] matrix) {
                List<int[]> ret = new ArrayList<>(); // 储存最终数据
                int m = matrix.length; // 获取矩阵一边的长度
                if(m < 1) return ret; // 矩阵大小为0时
                int n = matrix[0].length; // 获取矩阵另一边的长度
                boolean[][] Pacific = new boolean[m][n]; // 太平洋的
                boolean[][] Atlantic = new boolean[m][n]; // 大西洋的

                for(int i = 0; i < m; i++) { // 递归判断一条边
                    dfs(matrix, i, 0, Pacific, matrix[i][0]);
                    dfs(matrix, i, n-1, Atlantic, matrix[i][n-1]);
                }
                for(int i = 0; i < n; i++) { // 递归判断另一条边
                    dfs(matrix, 0, i, Pacific, matrix[0][i]);
                    dfs(matrix, m-1, i, Atlantic, matrix[m-1][i]);
                }

                for(int i = 0; i < m; i++) { // 取交集得到最终结果
                    for(int j = 0; j < n; ++j)
                        if(Pacific[i][j] && Atlantic[i][j])
                            ret.add(new int[]{i, j}); // 放入数据
                }
                return ret; // 返回结果
            }

            private void dfs(int[][] m, int x, int y, boolean[][] visited, int pre) {
                // 超出边界 或 判断过是可以的 或 不能继续向上流动，则返回
                if(x < 0 || y < 0 || x >= m.length || y >= m[0].length || visited[x][y] || m[x][y] < pre)
                    return;
                visited[x][y] = true; // 可以向上流
                dfs(m, x+1, y, visited, m[x][y]); // 递归判断相邻行或列
                dfs(m, x-1, y, visited, m[x][y]); // 递归判断相邻行或列
                dfs(m, x, y+1, visited, m[x][y]); // 递归判断相邻行或列
                dfs(m, x, y-1, visited, m[x][y]); // 递归判断相邻行或列
            }
        }

（3）总结

这个解题思路来看的话感觉还是可以的，就是会有一些奇怪的bug，不知道怎么肥四。

题目总结

这个题目难度比之前的大一些，不好做，包括写的时候也查了一些资料（运用不熟练），好在最后搞出来了（虽然有一些奇怪的bug）。

（递归真香）

最大正方形

大一 -> 大二暑期算法作业

分站已经上线简约风算法作业集合

看到题目的感想

寻找最大正方形是小时候经常玩的一种游戏，说是可以锻炼观察力与判断力什么的，现在也会有家长带着小孩玩这个游戏，不过不是很多。

题目描述

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]
输出：4

示例 2：

输入：matrix = [[“0”,”1”],[“1”,”0”]]
输出：1

示例 3：

输入：matrix = [[“0”]]
输出：0

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-square
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目解答

（ps：由于做题时采用的是执行代码，并未提交，提交结果均为后来补上，所以时间均为两天前）

1、暴力计算

（1）解题思路

语言描述不是很棒，大家凑活看叭，┭┮﹏┭┮

想了想，暴力计算是最简单直观的做法，具体做法如下：

遍历矩阵中的元素，当遇到 1时，将该元素作为正方形的左上角的位置。
确定正方形的左上角后，根据左上角所在的行和列计算可能的最大正方形的边长（正方形的范围- 不能超出矩阵的行和列），在该范围内寻找只包含 1 的最大正方形；
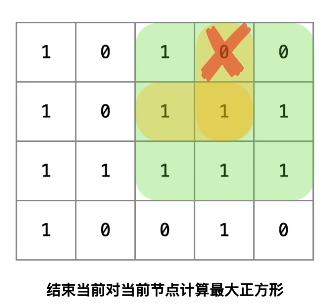
每次在下方新增一行以及在右方新增一列，判断新增的行和列是否满足所有元素都是 1。（方便起见，需要先判断选取的点的右下角的点是否为1。若不是，则跳出本次循环并储存当前的最大正方形，找到下一个元素是1的节点作为左上角点，重复2、3步；若是，则判断下一行和右一列的其他元素是否都为1 （注：这里不是下一行右一列的所有元素，而是初始左上角和以当前点为右下角的正方形的范围内的点，如下图） ，若不都为1，则跳出本次循环并储存当前的最大正方形，找到下一个元素是1的节点作为左上角点，重复2、3步；若都为1，则继续第3步）。

（2）代码

配合题目链接食用

java

class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) { // 没有矩阵或矩阵大小为0时
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') { // 遇到一个 1 作为正方形的左上角
                    maxSide = Math.max(maxSide, 1); // 更新可能的最大正方形边长
                    int currentMaxSide = Math.min(rows - i, columns - j); // 当前最大正方形边长
                    for (int k = 1; k < currentMaxSide; k++) { // 判断新增的一行一列是否均为 1
                        boolean flag = true;
                        if (matrix[i + k][j + k] == '0') { // 判断右下角的点
                            break;
                        }
                        for (int m = 0; m < k; m++) { // 判断下一行右一列
                            if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
                                flag = false;
                                break;
                            }
                        }
                        if (flag) { // 若判断都是1，则更新，不是则退出本次循环，寻找下一个左上角
                            maxSide = Math.max(maxSide, k + 1); // 更新可能的最大正方形边长
                        } else {
                            break;
                        }
                    }
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}

（3）总结

暴力的思路比其他方法简单（但是我的描述可能会有些不顺畅），但是效率不高。

2、dp算法（动态规划）（来自题解）

又一次见到了动态规划，还是有无从下手的感觉。

（1）解题思路

方法一虽然直观，但是时间复杂度太高，有没有办法降低时间复杂度呢？

可以使用动态规划降低时间复杂度。我们用dp(i,j) 表示以 (i,j) 为右下角，且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i,j) 的值，那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值，其平方即为最大正方形的面积。

那么如何计算 dp 中的每个元素值呢？对于每个位置 (i,j)，检查在矩阵中该位置的值：

如果该位置的值是 0，则 dp(i,j)=0，因为当前位置不可能在由 1 组成的正方形中；
如果该位置的值是 11，则 dp(i,j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加 1，状态转移方程如下：

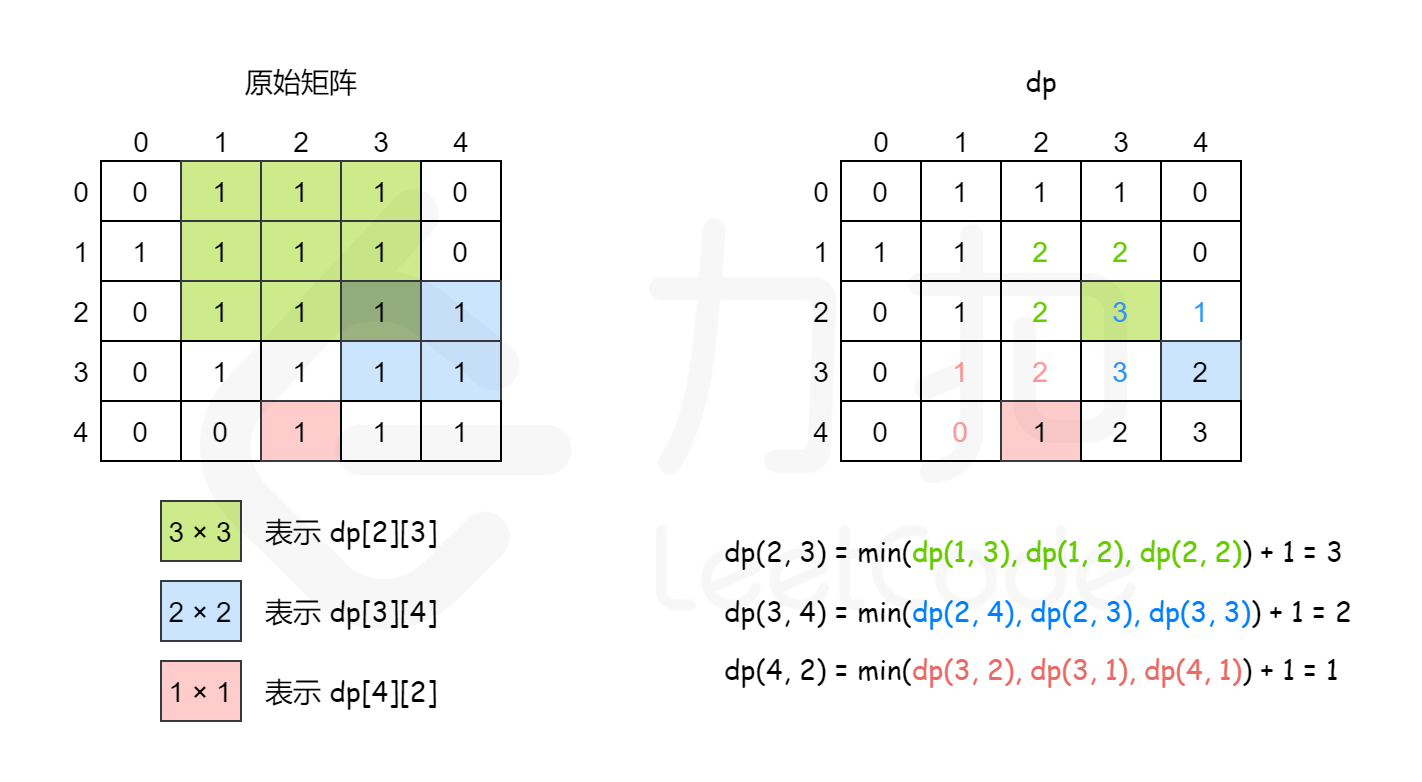
dp(i,j) = min( dp(i−1,j) , dp(i−1,j−1) , dp(i,j−1) ) + 1

如果读者对这个状态转移方程感到不解，可以参考 1277. 统计全为 1 的正方形子矩阵的官方题解，其中给出了详细的证明。

此外，还需要考虑边界条件。如果 i 和 j 中至少有一个为 0，则以位置 (i, j)(i,j) 为右下角的最大正方形的边长只能是 11，因此 dp(i,j)=1。

以下用一个例子具体说明。原始矩阵如下。

0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1
对应的 dp 值如下。

0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3

下图也给出了计算 dp 值的过程。

（2）代码

配合题目链接食用

Java

class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int[][] dp = new int[rows][columns];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    maxSide = Math.max(maxSide, dp[i][j]);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/maximal-square/solution/zui-da-zheng-fang-xing-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

C++

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return 0;
        }
        int maxSide = 0;
        int rows = matrix.size(), columns = matrix[0].size();
        vector<vector<int>> dp(rows, vector<int>(columns));
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    maxSide = max(maxSide, dp[i][j]);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/maximal-square/solution/zui-da-zheng-fang-xing-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（3）总结

动态规划解题的思想还需要学习，现在还上不了手。

题目总结

这次的题目是数最大正方形，暴力方法还是最先考虑到的，之后菜知道动态规划也可以解决。（动态规划现在还属实不会）

2021暑期算法作业合集

写在前面

二叉树的中序遍历

看到题目的感想

题目描述

题目解答

1.递归算法

（1）解题思路

（2）代码

C++

Java

C（来自题解）

（3）总结

2.迭代算法

（1）解题思路

（2）代码

C++

Java

C（来自题解）

（3）总结

3.Morris 中序遍历（来自题解）

（1）思路与算法

（2）代码

（3）总结

题目总结

爬楼梯

看到题目的想法

题目描述

题目解答

1.动态规划

（1）解题思路

（2）代码

C++

Java

C

（3）总结

2.斐波那契数列

（1）解题思路

（2）代码

C++

Java

C

（3）总结

3.矩阵快速幂（来自题解）

（1）解题思路 + 代码

（2）总结

题目总结

拓展（动态规划）（摘自题解）

动态规划应该如何debug

总结

原作者对本题总结

原作者的题目解答

罗马数字转整数

看到题目的想法

题目描述

题目解答

1.暴力解题

（1）解题思路

（2） 代码

（3）总结

2.模拟（来自题解）

（1）解题思路

（2）代码

C++

Java

（3）总结

题目总结

太平洋大西洋水流问题

看到题目的感想

题目描述

题目解答

逆流而上

（1）解题思路

（2）代码

Java

（3）总结

题目总结

最大正方形

看到题目的感想

题目描述

（2）代码