Leetcode-133-克隆图
# Leetcode 133. 克隆图
# 题目描述
给你无向连通图中一个节点的引用,请你返回该图的深拷贝(克隆)。
图中的每个节点都包含它的值 val ( int ) 和其邻居的列表( list[Node] )。
1 | class Node { |
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1( val = 1 ),第二个节点值为 2( val = 2 ),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
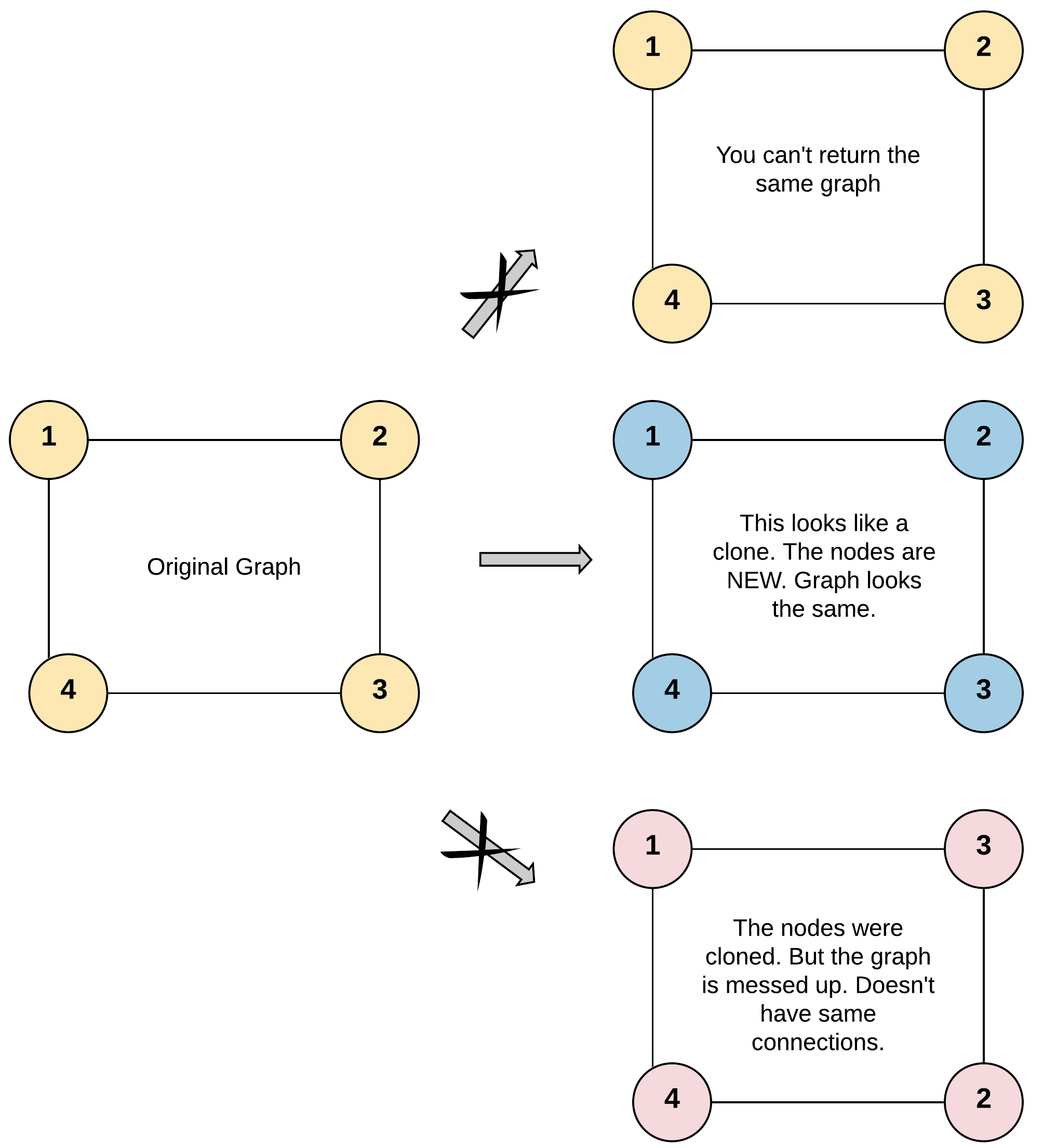
1 | 输入:adjList = [[2,4],[1,3],[2,4],[1,3]] |
示例 2:
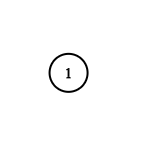
1 | 输入:adjList = [[]] |
示例 3:
1 | 输入:adjList = [] |
示例 4:
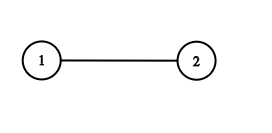
1 | 输入:adjList = [[2],[1]] |
提示:
- 节点数不超过 100 。
- 每个节点值
Node.val都是唯一的,1 <= Node.val <= 100。 - 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点
p是节点q的邻居,那么节点q也必须是节点p的邻居。 - 图是连通图,你可以从给定节点访问到所有节点。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/clone-graph
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
# 解题思路
对一个图进行深拷贝时,我们可以对它进行遍历,并在遍历时进行拷贝,最后得到该图的深拷贝结果。
通过一个节点遍历一个连通图的有效方法为深度优先遍历 (DFS) 和广度优先遍历 (BFS)。(层序遍历不适合无向图)
我们知道,无向图中,若 A、B 两点相连,则可以从 A 连接 B 也可以从 B 连接 A,这一点使得我们在使用深度优先遍历和广度优先遍历克隆 (深拷贝) 一个无向图时需要对结点进行标记,来代表它们是否已经被克隆过。
关于这一点的解决,最开始时想对每一个节点加一个 tag 来表示是否已经克隆过,后来发现不太行;之后也尝试了使用队列、栈和列表来实现 tag ,也没有达到想要的效果,最后选取了 ** 哈希表HashMap ** 来实现对克隆的记录。
在 HashMap 中, key / value 分别为 原始图节点 / 克隆图节点 ,这样表示比较清晰且便于查找 (也做过储存节点值 / 克隆图节点,但不如上文方法清晰)。我们从给定节点开始对图进行遍历。如果某个节点已经被访问过,则返回其克隆图中的对应节点 (查找 HashMap)。如果当前访问的节点不在哈希表中,则创建它的克隆节点并存储在哈希表中。注意:在需要递归的时候,克隆节点并保存在哈希表中的操作需要放在进入递归之前,不然有可能在递归中遇到相同的节点,陷入死循环 (再次遍历此节点)。
递归操作:在递归时,会递归每个节点的邻接点,递归次数由邻接点数量决定,每一次都返回对应邻接点的克隆节点 (注意:克隆前需要先判断该点是否已经被克隆过),最后返回这些克隆节点的列表,放入对应克隆节点的邻接表中,这样就可以克隆给定的节点和其邻接点。
# 1. 深度优先遍历(递归)
通过递归实现深度优先遍历,在遍历的中间对节点进行克隆并将克隆节点保存在哈希表中(注意克隆保存和进入递归的先后)
# 2. 广度优先遍历(栈)
用栈实现广度优先遍历,这种做法不需要递归,但仍需要在遍历的中间对节点进行克隆并将克隆节点保存在哈希表中
# 代码实现
# 1. 深度优先遍历(递归)
1 | /* |
# AC 截图:
# 2. 广度优先遍历(栈)
1 | /* |
# AC 截图:

# 题目总结
做完这个题之后,我感觉主要思路就是对该图进行遍历并同时深拷贝,无论哪种遍历方法都需要给节点打上 tag 来标志该节点是否被克隆过(通过哈希表实现)。在深度优先遍历中使用递归时需要注意操作的先后顺序(克隆保存和进入递归的先后),否则会陷入死循环;广度优先遍历则不需要担心这一点。









