# Leetcode 632. 最小区间

# 题目描述

你有 k 个 非递减排列 的整数列表。找到一个最小区间，使得 k 个列表中的每个列表至少有一个数包含在其中。

我们定义如果 b-a < d-c 或者在 b-a == d-c 时 a < c ，则区间 [a,b] 比 [c,d] 小。

示例 1：

输入：nums = [[4,10,15,24,26], [0,9,12,20], [5,18,22,30]]
输出：[20,24]
解释： 
列表 1：[4, 10, 15, 24, 26]，24 在区间 [20,24] 中。
列表 2：[0, 9, 12, 20]，20 在区间 [20,24] 中。
列表 3：[5, 18, 22, 30]，22 在区间 [20,24] 中。

示例 2：

1 2	输入：nums = [[1,2,3],[1,2,3],[1,2,3]] 输出：[1,1]

提示：

nums.length == k
1 <= k <= 3500
1 <= nums[i].length <= 50
-105 <= nums[i][j] <= 105
nums[i] 按非递减顺序排列

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/smallest-range-covering-elements-from-k-lists
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解题思路

在解题过程中我们可以将题目给的若干列表表示出来，这里以三个列表为例。

我们用线段表示这三个列表的区间，用红圈表示列表中的元素。表示如下：

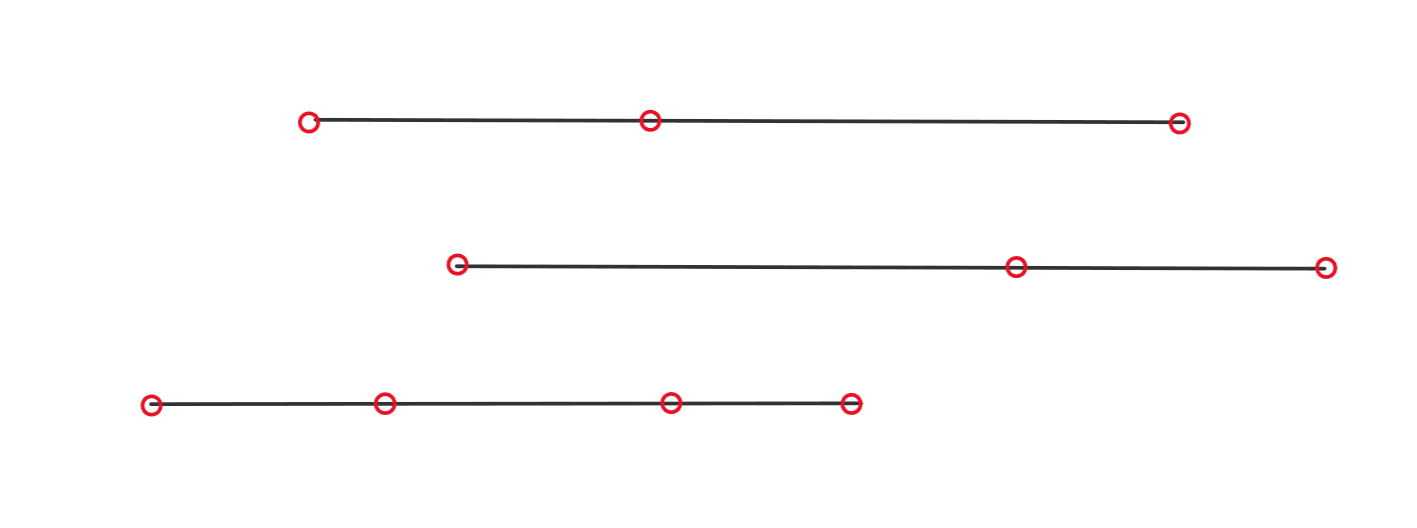
题目要求我们寻找一个区间，要求囊括每个有序列表中的至少一个元素。我们可以在上面画出的区间中画出非常多符合条件的区间，这里我们少画几个。画出的区间如下：

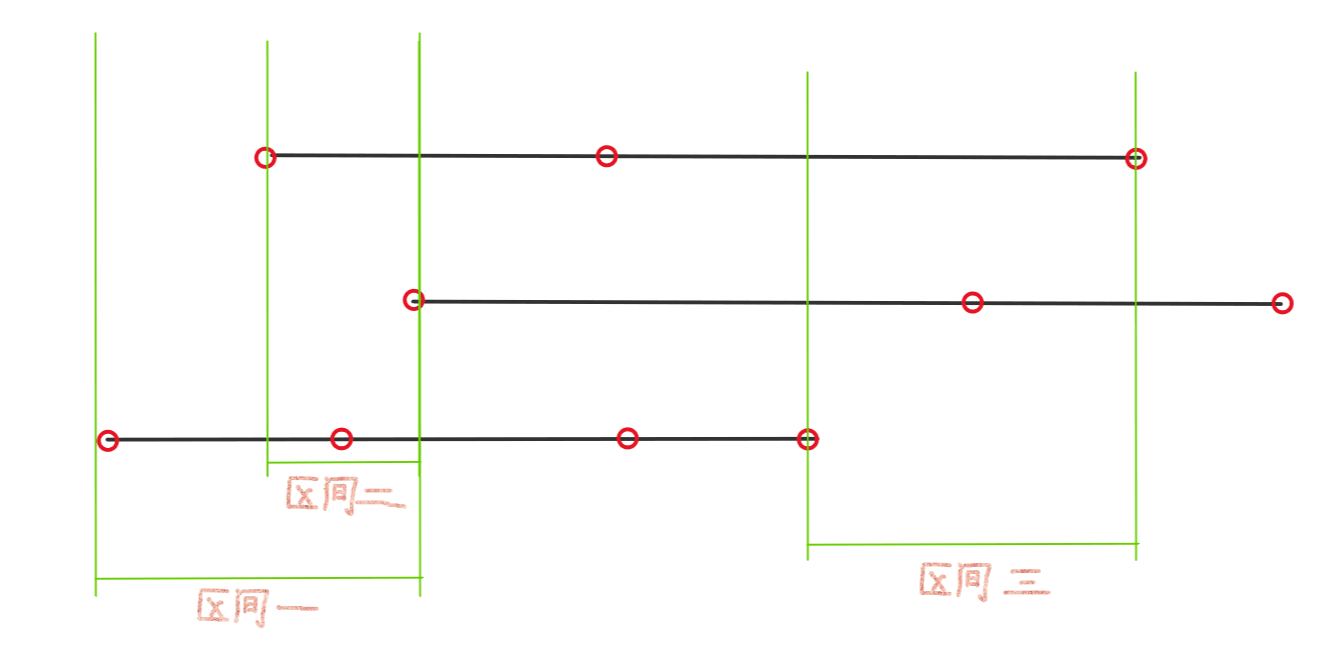
这里的 “至少一个元素” 可以理解成 “一个元素”，上图的区间一和区间二便是如此。因此，我们要寻找的最小区间只需要包含每个有序列表内的一个元素即可，于是我们得到了区间二和区间三。

那么，对于区间二和区间三，我们如何判断它们当中谁是我们要找的最小区间呢？那一定是这个区间内所包含的 3 个 ( k 个) 元素中，最小值和最大值的差值最小的那一个，这也就代表了这个区间最小。显然，区间二中最大值与最小值的差值小于区间三中最大值与最小值的差值，所以区间二比区间三要小。如果两个区间中最大值与最小值的差值相等，则数值小的区间小（参照题目中的条件：我们定义如果 b-a < d-c 或者在 b-a == d-c 时 a < c ，则区间 [a,b] 比 [c,d] 小）。

现在我们以 nums = [[2,4,7],[1,4,5],[3,5,6,8]] 作为示例来思考如何寻找最小区间。

我们先将这三个列表画出来，如下图所示：

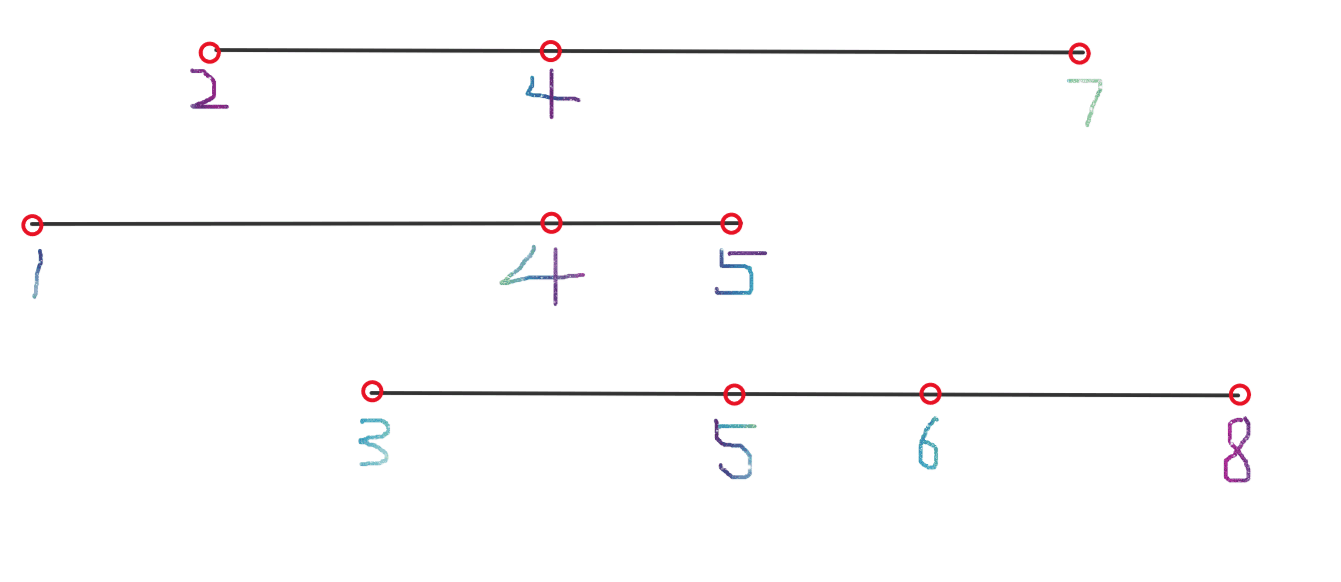
我们可以为每个列表定义一个指针，如图：

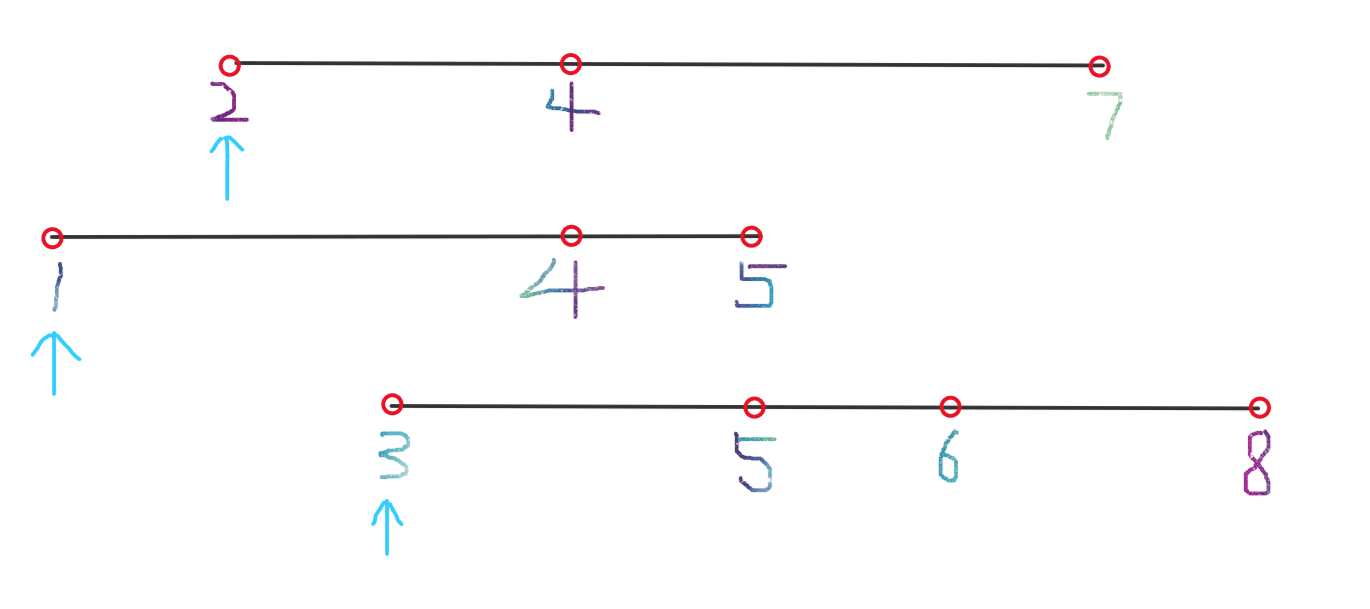
此时，这三个指针所指的三个元素可以构成一个最小区间，且最小值与最大值的差值为 2，我们先记录下来。

接下来我们寻找最小区间，如何寻找呢？我们可以将此时的左边界右移来缩小区间，计算右移后的区间长度，发现和上一个区间的长度相同，并且上一个区间的数值更小，所以此次移动后不记录区间长度；右移之后如图所示：

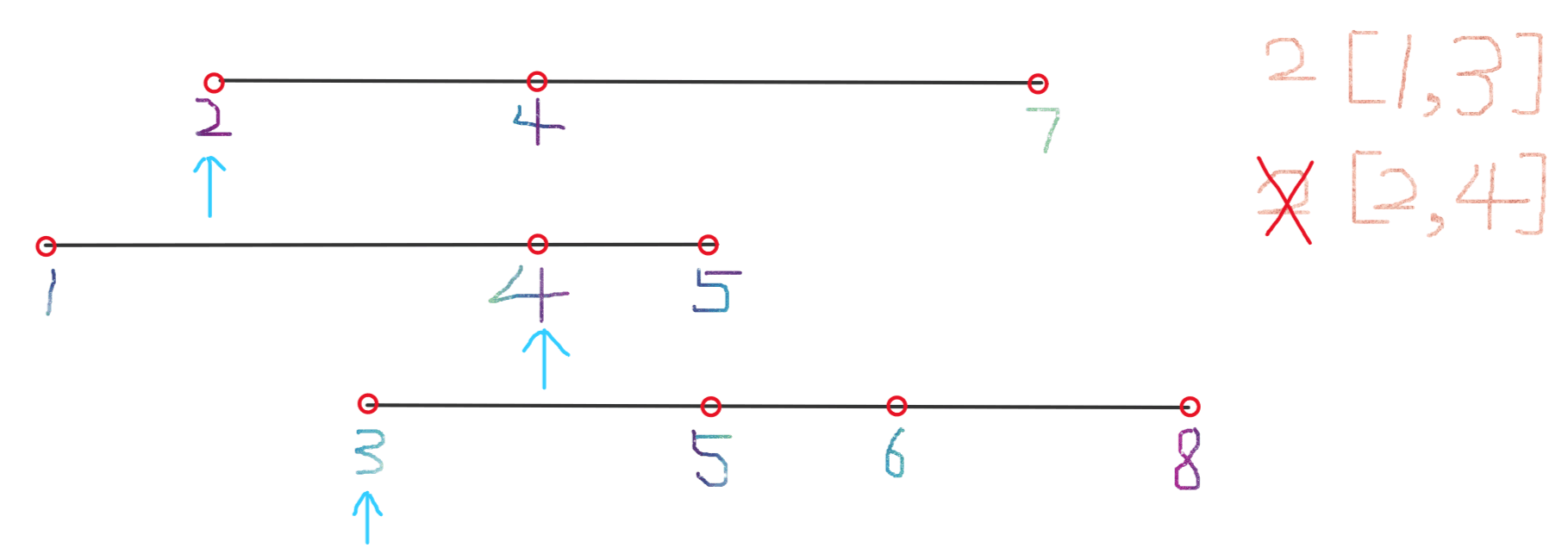
再次将左边界右移来缩小区间，计算右移后的区间长度并记录；右移之后如图所示：

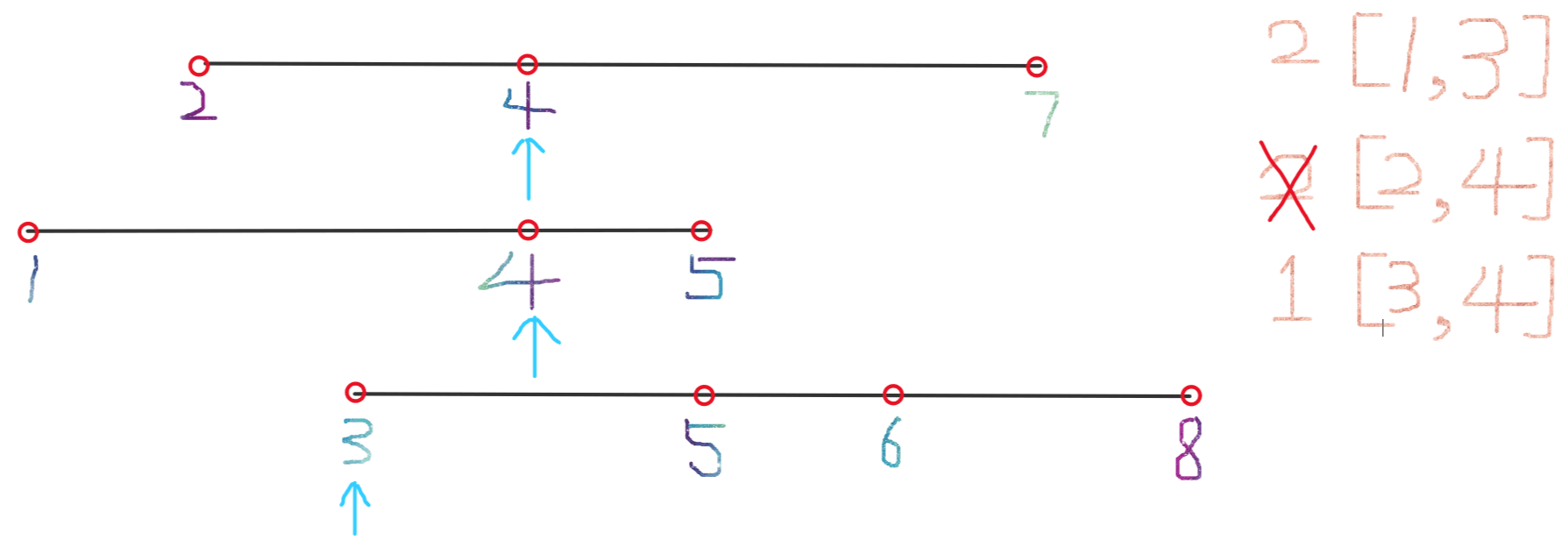
再次将左边界右移来缩小区间，计算右移后的区间长度，发现和上一个区间的长度相同，并且上一个区间的数值更小，所以此次移动后不记录区间长度；右移之后如图所示：

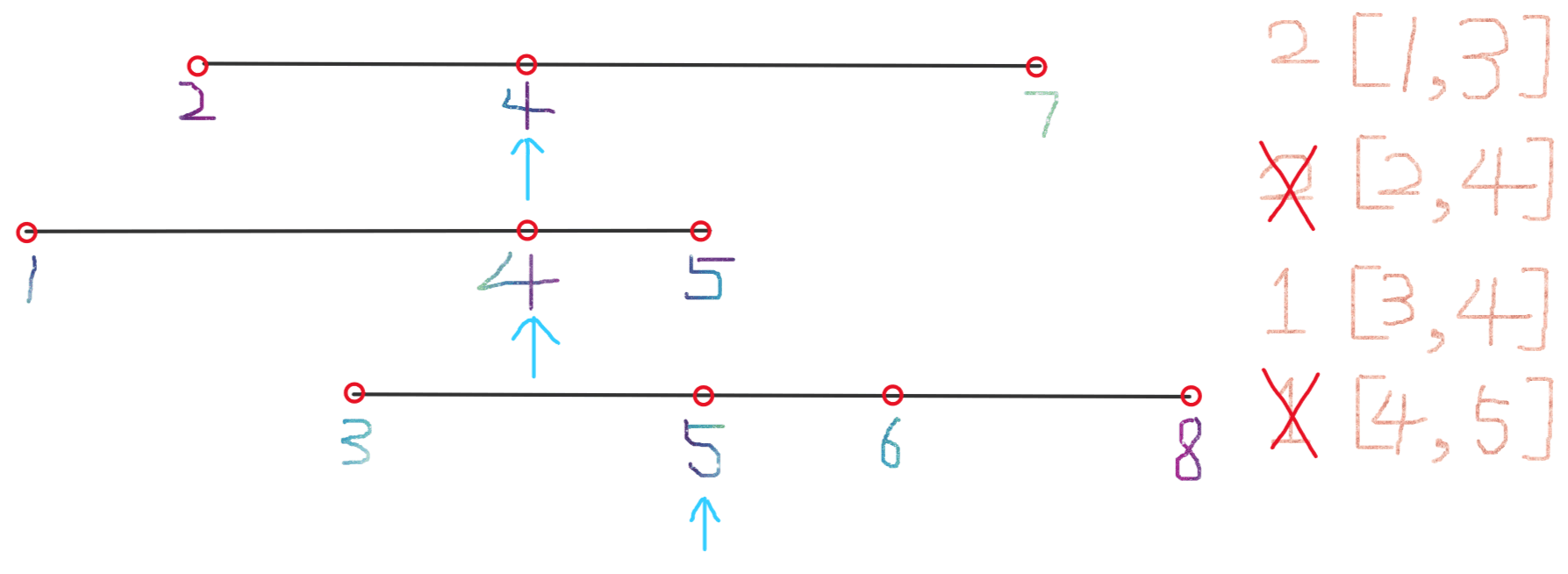
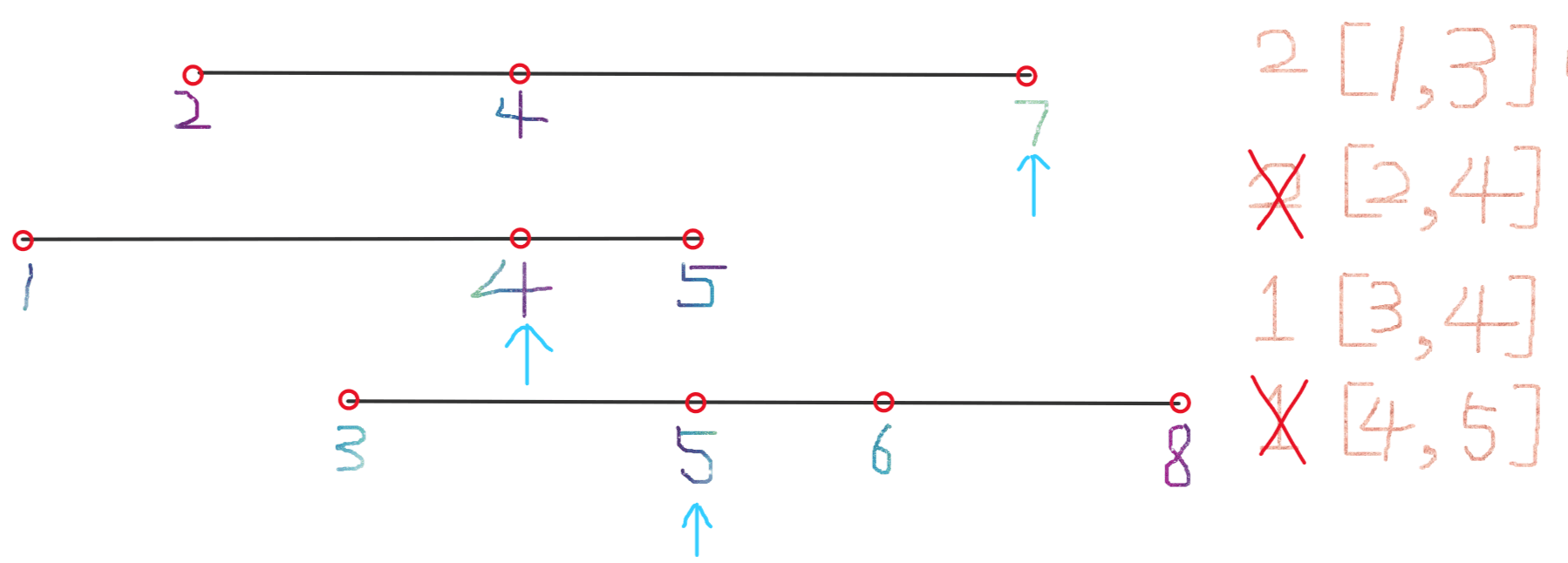
再次将左边界右移来缩小区间，计算右移后的区间长度，发现大于之前的区间长度，不记录；右移之后如图所示：

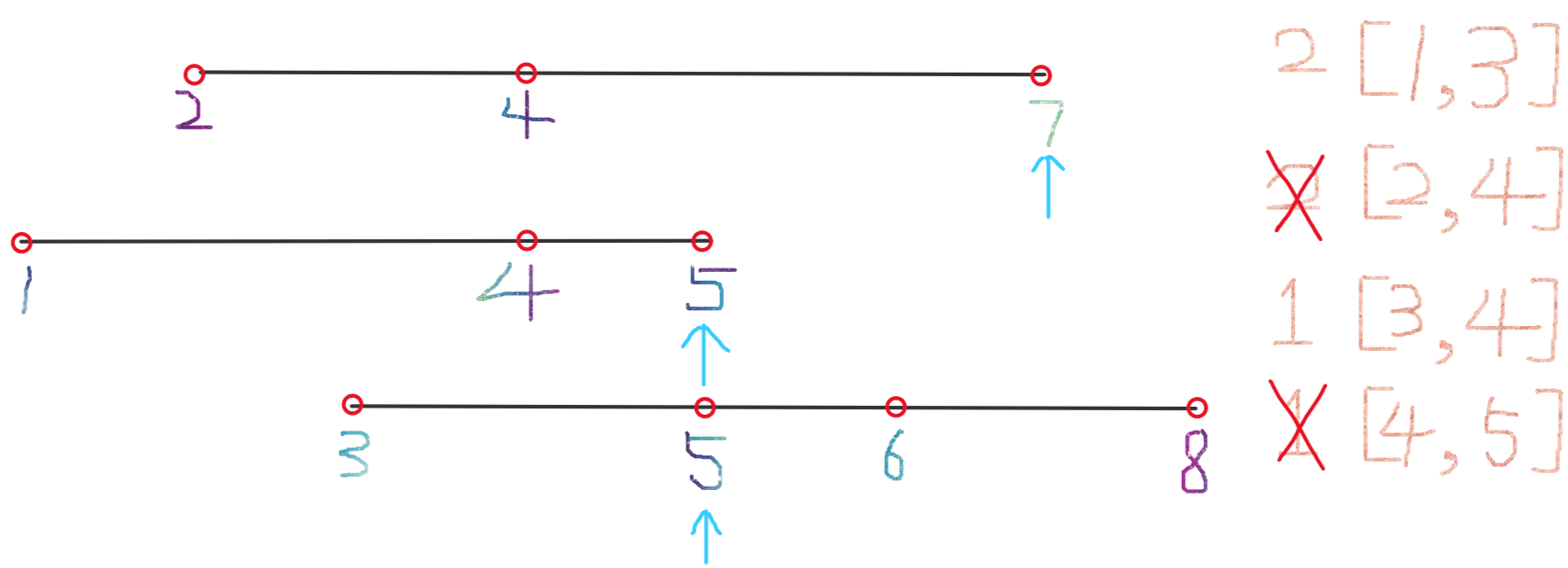
此时，第二个列表已经走到最后，左边界将无法移动，此时所记录的最小区间即为我们要寻找的最小区间，即最小区间为 [3,4] 。

# 代码实现

前面列举了两种暴力解答的方法（未实现），后面为上方解题思路的代码

import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;

import static java.lang.Math.*;

class Solution {
    // 一、暴力解答：遍历每个数组，计算每个数组中出现的每个数字在所有数组中出现过的数组个数
	// 全部出现的元素组成的最短区间即为想要的结果

	// 二、穷举：每个元素作为头和尾，然后判断是否符合条件之后判断是否最短

	// 每次向右移动最小值，记录最短区间长度和位置
	// 长度短 或 长度相同时数值小 的区间小
    public int[] smallestRange(List<List<Integer>> nums) {
//        定义一个模拟区间，最开始范围是 -1e-5 到 1e-5
        int leftRange = (int)-1e-5;
        int rightRange = (int)1e5;
        int minRange = rightRange - leftRange;

//        当前区间内的最大值(选取1e-5结果不对)
        int max = Integer.MIN_VALUE;

// 索引0，代表第一个链表；ptrs[0] = 指针在链表中的位置
        int size = nums.size();
        int[] ptrs = new int[size];

//        定义一个优先队列，用来取最小值（也可以用for循环代替）
//        优先队列可以通过 ptrs[index*] 把所有指针所指位置最小的指针放到前面去，从而取到最小值
        PriorityQueue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
            public int compare(Integer index1, Integer index2) {
                return nums.get(index1).get(ptrs[index1]) - nums.get(index2).get(ptrs[index2]);
            }
        });

//      开始时，将索引都赛道队列中，并取下 [max,nums.get(i).get(0)] 区间的最大值
        for (int i = 0; i < ptrs.length; i++) {
            queue.offer(i);
            max = max(max, nums.get(i).get(0));
        }

//      循环更新，直到某一区间走完
        while (true) {
//          取出最小值（左边界）（也可以用for循环代替）
            int minIndex = queue.poll();
//          计算当前范围
            int curRange = max - nums.get(minIndex).get(ptrs[minIndex]);
//          如果当前范围小，则更新左右边界
            if (curRange < minRange) {
//              更新右边界
                minRange = curRange;
//              左边界是当前值最小的索引（在优先队列的最前面）
                leftRange = nums.get(minIndex).get(ptrs[minIndex]);
                rightRange = max;
            }
//          指针右移
            ptrs[minIndex]++;
//          指针超出，跳出循环
            if (ptrs[minIndex] == nums.get(minIndex).size())
                break;

//          将最小值放入
            queue.offer(minIndex);
//          取得当前区间的最大值
            max = max(max, nums.get(minIndex).get(ptrs[minIndex]));
        }
//      构造结果并返回
        int[] result = new int[2];
        result[0] = leftRange;
        result[1] = rightRange;
        return result;
    }
}